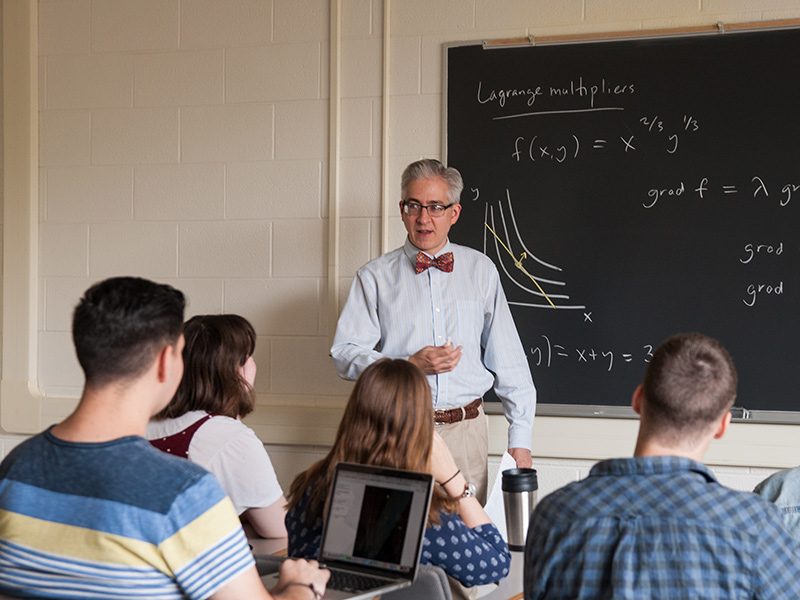
Build a solid foundation in mathematics, then choose to specialize in applied, theoretical,
or pure mathematics. Individualize your academic experience by combining mathematics
with other subjects like physics, information technology, and art.
Or, take courses in related programs like accounting, data science, and economics
to expand your knowledge. Juniata mathematics alumni pursue careers in a variety of
fields including actuarial science, government, finance, education, and more.
Juniata mathematics alumni pursue careers in a variety of fields including actuarial science, government, finance, education, and more.
Build a solid foundation in mathematics, then choose to specialize in applied, theoretical,
or pure mathematics. Individualize your academic experience by combining mathematics
with other subjects like physics, information technology, and art.
Or, take courses in related programs like accounting, data science, and economics
to expand your knowledge. Juniata mathematics alumni pursue careers in a variety of
fields including actuarial science, government, finance, education, and more.
Juniata mathematics alumni pursue careers in a variety of fields including actuarial science, government, finance, education, and more.
Build a solid foundation in mathematics, then choose to specialize in applied, theoretical,
or pure mathematics. Individualize your academic experience by combining mathematics
with other subjects like physics, information technology, and art.
Or, take courses in related programs like accounting, data science, and economics
to expand your knowledge. Juniata mathematics alumni pursue careers in a variety of
fields including actuarial science, government, finance, education, and more.
Juniata mathematics alumni pursue careers in a variety of fields including actuarial science, government, finance, education, and more.

Individualize

Individualize

Individualize

Individualize
Research

Research

Research

Research


Experience

Experience

Experience

Experience
Study Abroad
Students in the past have taken upper level mathematics courses from the University of Edinburgh (Scotland) through the St. Andrews Society Scholarship, the University of Newcastle (Australia) and the University of Leeds (England). Other excellent opportunities are the Budapest semesters in Hungary and the Math in Moscow program at the Independent University of Moscow where all courses in both programs are taught in English. International partners that offer upper level mathematics courses also include the University of the Gambia (Africa) and the University of Waikato (New Zealand).
 skip to content
skip to content







